Riccardo Carini (Imperial College London - LSGNT)
17:00 - 18:00 • King's College, Strand Building, Room S-3.20 • 18 November 2021
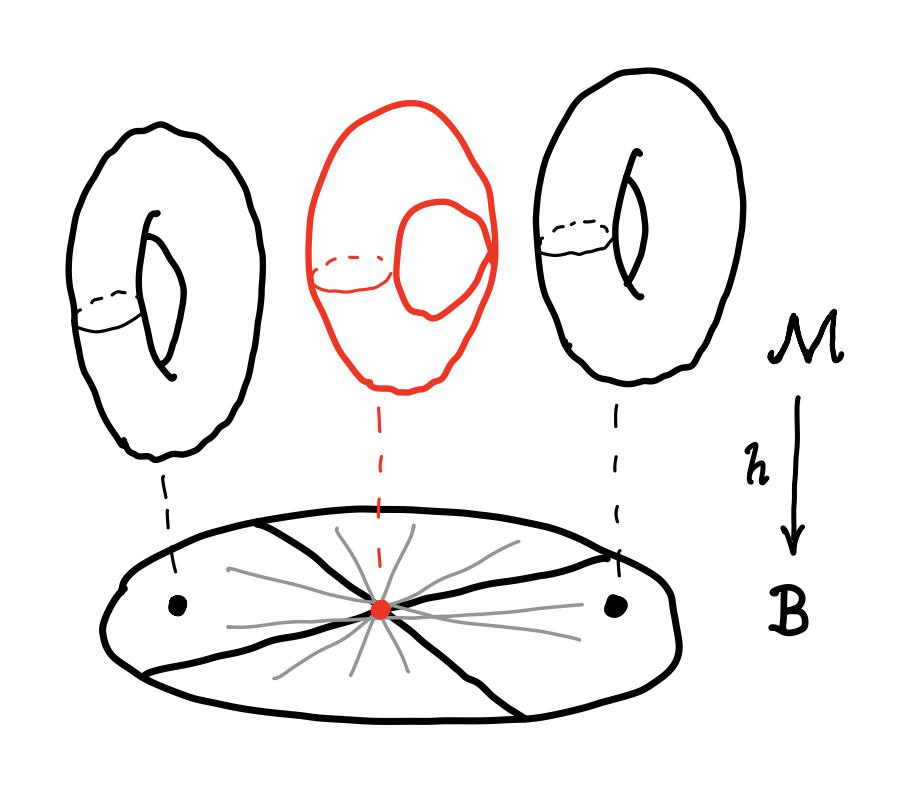
Introduction to Higgs bundles and the Hitchin map
17:00 - 18:00 • King's College, Strand Building, Room S-3.20 • 18 November 2021
Abstract:
Higgs bundles were first introduced by Hitchin in the 80’s in the study of Yang-Mills self-duality equations. Since then, they have become central objects of study in Kähler and hyperkähler geometry, representation theory (via nonabelian Hodge theory) and, more recently, mirror symmetry. I will mainly focus on the geometry of the Hitchin map and the related spectral correspondence, which realises the moduli space of Higgs bundles on a given curve Σ as a relative Jacobian of a family of covers of Σ.