Job
Steps In DMAREL - Unit Cell And Defects Setup
This section reads in the unit cell. Three directives must be given in
the order (For DMAREL)
REGION RADII AND CUTOFFS
| Operand types | F | F | F | F |
| Operand names | RLAT | CUTPOT | CUTSHL | ACCTH |
| Operand types (continued) | F | < F > | for future use | for future use |
| Operand names (continued) | CUTTH | KMAX |
CUTO directive is usedto define the length cale for all distances used in the calculation. This parameter controls the partition of the Ewald sum betweenreal and reciprocal space parts and the most efficient partition will results if a length scale of roughly the cube root of the cell volume is chosen. In most crystals simply using the c-vector magnitude will fulfil this requirement. Often it is more convenient to choose a length scale of 1 Å to make the input file simpler to understand, no loss of accuracy will result from this but the program may take a little longer to carry out the Ewald sum as the partitioning between real and reciprocal space sums will not be optimal.
The cutoff distance for the short range potentials is also inut on the CUTO line. This parameter is input in units of the length scale.
The genal format for the CUTO directive is:
| CUTO <length_scale> <short_range_cut_off> | ||
| Variable | Type | Units |
| <length_scale> | real | Å |
| <short_range_cut_off> | real | length scale units |
For example if a crystal has a c-vector of 3.806 Å and you require a cut off for the short range potentials of 15 Å, there are two possibilities:
(1) CUTO 3.806 3.941(2) CUTO 1.0 15.0
In the first case, the c-vector itself will be used as the program's length scale and much of the remaining input (the lattice vectors, atom positions etc.) will have to be input in this length scale. The second alternative uses 1 Å as the chosen length scale so that subsequent input data will simply be in Angstrom units.
RDMA is a cutoff for all electrostatic above charge dipole, and it normally takes the value the same as the 2nd value of CUTO.
- RLAT
CUTPOT
- This gives the short range potential cutoff in lattice units. See Preliminary Comments for a description of the use of cutoffs. CUTPOT should not be equal to an interatomic distance in the crystal. This is because the test in the perfect lattice calculation may find one bond but leave out a symmetry related bond, giving perfect lattice tensor properties of the wrong symmetry. Usually it is safe just to ensure that CUTPOT does not equal an integral number of lattice vectors. (i.e. that CUTPOT is not an integer).
Printed output
C-vector magnitude= RLAT Angstroms Cut off for short range potentials = Cutpot Angstroms
LATTICE VECTOR INPUT
| Operands | none |
This directive is required. The LATT directive instructs the program to call the lattice vector input routine. This reads in three records. The format of each record is 3F Each record refers to one lattice vector, and gives the orthonormal x, y, zcoordinates of the lattice vectors. The orthonormal lattice vector components must be given to a sufficiently high precision for all the symmetry elements of the lattice point group to be found. By default, at least seven significant figures must be given, unless the ACCU directive is used. (See examples after the BASI directive).
The following section describes how to calculate orthonormal lattice vectors from the conventional crystallographic unit cell. Firstly the general case will be given, although this should normally only be used for triclinic and monoclinic unit cells. The matrix given below (the normalising matrix N) defines an orthonormal coordinate system with the z axis parallel to the crystallographic c axis, the x axis parallel to the reciprocal a axis and the y axis forming a right-handed set with x and z. The matrix is normalised so that one unit = the crystallographic c spacing. This value should therefore be used for the value RLAT on the REGI directive.
 |
(1) |
The unit cell is
defined by three cell lengths a, b, c, and by three
angles a, b, g.
a* above is the length of the reciprocal a lattice
vector. A general expression for the length of a* is
|
|
(2)
|
|
|
(3)
|
|
|
(4)
|
Whilst this matrix will work for any crystal, care is needed if comparison is to be made with perfect lattice tensor properties. (Elastic and dielectric constants). These will have been measured with respect to an orthogonal coordinate system which is not necessarily the same as that given above. Reference to the experimental papers may be necessary to find out the coordinate system used to measure the tensor properties. The above matrix should be used for triclinic and monoclinic crystals. For tetragonal, orthorhombic and cubic crystals a simpler matrix is used, which defines x parallel to a instead of a*.
 |
(5) |
For trigonal and hexagonal crystals, x is again defined parallel to A giving the matrix
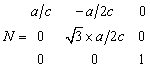 |
(6) |
The normalising matrix N defined above will transform any vector defined in crystallographic units into orthonormal coordinates. The vector may be a unit cell vector or a basis atom vector. If the unit cell is primitive, (P), the unit cell vectors in crystallographic coordinates are simply given by the identity matrix.
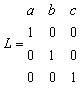 |
(7) |
Multiplying this by the normalising matrix N forms the orthogonal lattice vectors
|
|
(8) |
Hence the columns of the normalising matrix given above are the lattice vectors needed by DMAREL. Note that the input to DMAREL and the printed output from DMAREL give the lattice vectors in rows, so the normalising matrix given above will be transposed.
If the unit cell
is centred, then the centred lattice vectors should be used. It is recommended
that this is always done. The non-primitive cell may be used, and the
same answers will be produced. However there will be more basis atoms
per unit cell if this is done, and the perfect lattice calculation will
take correspondingly longer to run. The centred lattice vectors in crystallographic
units may conveniently be taken as the columns of the matrices L
given in the following table (Other choices are possible).
| Centring type | A | B | C | ||||||
| A | 1 | 0 | 0 | ||||||
| 0 | 1 | 1/2 | |||||||
| 0 | 0 | 1/2 | |||||||
| B | 1 | 0 | 1/2 | ||||||
| 0 | 1 | 0 | |||||||
| 0 | 0 | 1/2 | |||||||
| C | 1 | 1/2 | 0 | ||||||
| 0 | 1/2 | 0 | |||||||
| 0 | 0 | 1 | |||||||
| I | -1/2 | 1/2 | 1/2 | ||||||
| 1/2 | -1/2 | 1/2 | |||||||
| 1/2 | 1/2 | -1/2 | |||||||
| F | 0 | 1/2 | 1/2 | ||||||
| 1/2 | 0 | 1/2 | |||||||
| 1/2 | 1/2 | 0 | |||||||
| R | 2/3 | -1/3 | -1/3 | ||||||
| 1/3 | 1/3 | -2/3 | |||||||
| 1/3 | 1/3 | 1/3 |
The orthonormal
lattice vectors required by DMAREL are then formed by the matrix product
![]() .
.
Again the matrix O must be transposed to be input to DMAREL.
The lattice vectors are defined as follow:
| LATT | ||
|
|
|
|
|
|
|
|
|
|
|
|
| Variable | Type | Units |
| <each_component> | real | length scale units |
There is no ENDS statement associated with this directive.
Printed output
The lattice vectors are always printed by default. They are printed in rows, with thex, y, z components of each lattice vector in each row. If PRIN LATT MPRINT with MPRINT=1 is used, the reciprocal lattice vectors are also printed, again in rows.
Error messages
ERROR - THE LATTICE VECTORS ARE COPLANARThis is a fatal error. The program decided that the lattice vectors are coplanar by working out the volume of the unit cell, which is equal to the determinant of the lattice vector matrix. This is tested to see if it is greater than ACCLAT (see ACCU directive).
ERROR - LATTICE VECTOR N INCORRECTLY READ.A fatal error, there is a format error on the Nth lattice vector input record.
BASIS ATOM INPUT
DATA INPUT
BASI
| Operands | none |
The BASI
directive instructs the program to call the basis atom input routine.
This reads in further records, which have one of three possible formats
| Card format | 2A | 3F | < I > |
| Species label | species coordinates | Optional molecule number | |
| Card format | A | 3F | |
| CENT | Point group origin | ||
| Card format | A | ||
| ENDS |
Only one CENT and ENDS record is permitted. The CENT record defines the basis origin. This record is not required for DMAREL, it may be omitted, in which case the basis origin is taken as the point 0.0 0.0 0.0. The ENDS record must be the last record, and instructs the subroutine to return to the main menu of directives.
There may be any number of species records up to a maximum of 500 (this includes the CENT record if present). The species label consists of two A4 fields (separated by a space). The first A4 field contains a species name, which must be unique for each atom type. (For example: NA+ CL- AL3+). The second field contains the word CODA that the species is an atom with a distributed multipole. Similar comments apply about the precision as for the lattice vectors, namely the coordinates must be given to at least 7 significant figures unless the ACCU directive has been used. The optional molecule number is used to indicate to which molecule it belongs. A value of zero, or leaving out the parameter all together, implies that intramolecular potentials will not be applied to this species, and is used for isolated ions.
The following section will describe how to generate the basis coordinates from the crystallographic coordinates. Usually only one equivalent position of a set of equivalent positions will be given in an experimental report. The coordinates of the equivalent positions are given in the International Tables for Xray Crystallography. The coordinates of all the equivalent positions may therefore be determined in crystallographic units. If centred lattice vectors have been used then the basis atoms generated by the centring vectors must not be given. The coordinates are normalised using the normalising matrix N described in the LATT directive. If d is a basis atom vector in crystallographic coordinates the orthonormal basis vector e will be
|
|
(9) |
(See examples following this section.)
It should be noted that adding or subtracting a lattice vector, or an intergal multiple of a lattice vector, to a basis vector will have no effect on the program. In other words, basis atoms need not all be in the same unit cell. There used to be a limitation on this if the molecule option is being used. In this case, all the atoms of one molecule should be input such that the molecule can be generated without translating any of its component atoms by lattice vectors. However this limitation has now been removed.
The basis species will be sorted into an internal program order. In some cases it is necessary to know the sorted order in order to interpret the printed output. The sorted order may be printed using PRIN BASI 1. Alternatively, the basis species may be input in the sorted order so that no sorting occurs. The order into which they are sorted is determined by a number of rules.
(1) All atoms in molecules come before free ions.
(2) All species of the same type are sorted together.
The Ewald parameter h is also calculated at this point, according to the formula [!!]
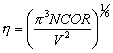 |
(10) |
where
- NCOR = Number of atoms in the unit cell
- VC = Volume of the unit cell in (cubic lattice units).
- This is used with the parameter ACCMAD (see ACCM directive) to define the cutoffs in direct and reciprocal space for the Ewald sums.
|
|
(11) |
|
|
(12) |
|
|
(13) |
Printed output
THE BASIS SPECIES ARE AS FOLLOWS ALL QUANTITIES ARE IN LATTICE UNITS NO. ORTHOGONAL COORDINATES LABEL MOLECULE
index x y z Label molecule
Origin of basis
The basis species and basis origin are printed as input by default. PRIN BASI -1 will suppress printing of the basis species. PRIN BASI 1 will print additionally the basis species after sorting and after the defect origin vector has been subtracted from them.
CUTOFF VALUE FOR DIRECT LATTICE SUM = X LATTICE UNITS
CUTOFF VALUE FOR RECIPROCAL LATTICE SUM = Y RECIPROCAL LATTICE UNITS
VALUES OF THE CONSTANTS USED IN THESE SUMMATIONS ARE Z1 Z2
This message is printed
by default. The constants Z1 and Z2 are hand
![]() .
.
Error messages
ERROR - LATTICE VECTORS NOT DEFINED BEFORE CRYSTAL BASISA LATT directive has been omitted or placed out of order, it should occur before the BASI directive.
ERROR - MAXIMUM OF MAXBAS BASIS SPECIES EXCEEDEDThis error does not cause the program to terminate immediately.
ERROR - UNIDENTIFIED SPECIES IN LATTICE BASISA species label has been found with a second A4 field which is not CODA.
ERROR - BASIS SPECIES i AND j ARE AT EQUIVALENT LATTICE SITES.Two basis species have been found at the same lattice site. They may be at the same lattice site translated by an integral number of lattice vectors, so the coordinates are not necessarily the same.
EXAMPLES OF LATTICE VECTOR AND BASIS ATOM INPUT
Example 1. NaCl O4
The data are taken from [!!]. The structure is orthorhombic with a side-centred unit cell (space group Cmcm).
| A = 7.085 | B = 6.526 | C = 7.048 |
| a = 0 | b = 0 | g = 90 |
First of all we must set up the lattice vectors. Normalising so that c = 1 lattice unit, and hence RLAT = 7.048 (see REGI directive), the normalising matrix N will be
 |
(14) |
The normalising matrix given above could be used as the non-primitive lattice vectors. However, it is desirable to always use primitive lattice vectors if possible as this reduces the number of basis atoms per unit cell, in this case by a factor of two. Referring to the LATT directive, the primitive lattice vectors for a C-centred structure are
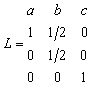 |
(15) |
The lattice vector matrix L defines the primitive lattice vectors as fractions of the unit cell lengths. The orthonormal lattice vectors are found by multiplying L by the normalising matrix N, giving
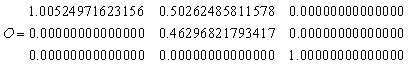 |
(16) |
The columns of this matrix are the lattice vectors needed by DMAREL, hence the matrix must be transposed to be input to DMAREL giving
| LATT | ||||
| 1.00524971623156 | 0.00000000000000 | 0.00000000000000 | ||
| 0.50262485811578 | 0.46296821793417 | 0.00000000000000 | ||
| 0.00000000000000 | 0.00000000000000 | 1.00000000000000 |
Turning now to the
basis atoms, there are four inequivalent basis atoms per unit cell.
|
Atom
|
Site
|
Wyckoff | |||||||||
|
type
|
symmetry
|
notation |
x
|
a
|
y
|
b
|
z
|
c
|
|||
|
Na
|
m2m
|
4c |
0
|
0
|
0
|
6637
|
0
|
25
|
|||
|
Cl
|
m2m
|
4c |
0
|
0
|
0
|
1683
|
0
|
25
|
|||
|
O
|
m.
.
|
8f |
0
|
0
|
0
|
2989
|
0
|
0867
|
|||
|
O
|
.
. m
|
8g |
0
|
1638
|
0
|
0384
|
0
|
25
|
Thus there will be 4 Na and Cl atoms and 8 of each of the inequivalent O atoms per unit cell. Note that these numbers refer to the full non-primitive unit cell so that by using the primitive cell we can reduce this by a factor of 2. The equivalent positions for these sites may be found in the International Tables for Xray Crystallography. We do not need to put in equivalent positions generated by adding the 1/2 1/2 0 vector since we have taken care of these by using primitive lattice vectors. Thus we have
|
4c
|
0
|
y
|
1/4
|
0
|
-y
|
3/4
|
|
8f
|
0
|
y
|
z
|
0
|
-y
|
z+1/2
|
|
0
|
y
|
-z+1/2
|
0
|
-y
|
-z
| |
|
8g
|
x
|
y
|
1/4
|
-x
|
-y
|
3/4
|
|
-x
|
y
|
1/4
|
x
|
-y
|
3/4
| |
Thus we can write
down the coordinates of the 2 Na atoms, the 2 Cl atoms and 4 for each
of the O atoms. Finally we need to multiply each of these vectors by the
normalising matrix defined above, giving the final set of coordinates
to be input to the program as
| BASI | ||||
| NA+ | CORE | 0.50262485811578 | 0.15157579455165 | 0.25000000000000 |
| NA+ | CORE | 1.00524971623156 | 0.31139242338252 | 0.75000000000000 |
| CL- | CORE | 1.00524971623156 | 0.15583510215664 | 0.25000000000000 |
| CL- | CORE | 0.50262485811578 | 0.30713311577753 | 0.75000000000000 |
| OX | CORE | 1.00524971623156 | 0.27676240068104 | 0.08670000000000 |
| OX | CORE | 0.50262485811578 | 0.18620581725312 | 0.58670000000000 |
| OX | CORE | 1.00524971623156 | 0.27676240068104 | 0.41330000000000 |
| OX | CORE | 0.50262485811578 | 0.18620581725312 | 0.91330000000000 |
| OX | CORE | 0.16465990351873 | 0.03555595913734 | 0.25000000000000 |
| OX | CORE | 1.34321467082860 | 0.42741225879682 | 0.75000000000000 |
| OX | CORE | 0.84058981271283 | 0.03555595913734 | 0.25000000000000 |
| OX | CORE | 0.66728476163451 | 0.42741225879682 | 0.75000000000000 |
Note that some of the coordinates given above have had lattice vectors added on so that all the basis atoms fall in the same unit cell. It is not essential to do this.
Example 2. Al2O3
The structure is
rhombohedral, space group D3d6(![]() ).
).
| A = | B = 4.75855 | C = 12.9906 |
| a = 0 | b = 90 | g = 120 |
Rhombohedral structures are always input in hexagonal coordinates with a centred unit cell. Normalising so that 1 lattice unit = c axis spacing (RLAT = 12.9906) gives the following normalising matrix, which are the lattice vectors of the non-primitive cell.
 |
(17) |
Referring now to the LATT directive, we see that a convenient choice of primitive lattice vectors in crystallographic units is
 |
(18) |
Multiplying by the normalising matrix N gives the primitive lattice vectors in orthonormal coordinates O. This matrix must be transposed to input into DMAREL, giving the matrix given below
| LATT | |||
| 0.18315358797900 | 0.10574377332272 | 0.33333333333333 | |
| -0.18315358797900 | 0.10574377332272 | 0.33333333333333 | |
| 0.00000000000000 | -0.21148754664544 | 0.33333333333333 |
The coordinates of the basis atoms in crystallographic units are
|
Atom
|
Site
|
Wyckoff
|
|||||||||
|
type
|
symmetry
|
notation
|
x
|
a
|
y
|
b
|
z
|
c
|
|||
|
Al
|
3.
|
12c
|
0
|
0
|
0
|
0
|
0
|
35200
|
|||
|
O
|
.
2
|
18e
|
0
|
3064
|
0
|
0
|
0
|
25
|
Referring to the International Tables for Xray Crystallography,
we find that the equivalent positions are
|
12c
|
0
|
0
|
z
|
0
|
0
|
-z+1/2
|
|
0
|
0
|
-z
|
0
|
0
|
z+1/2
|
|
|
18e
|
x
|
0
|
1/4
|
0
|
x
|
1/4
|
|
-x
|
-x
|
1/4
|
-x
|
0
|
3/4
|
|
|
0
|
-x
|
3/4
|
x
|
x
|
3/4
|
This allows us to write down the coordinates (in crystallographic units) of the 4 aluminium and 6 oxygen atoms. Finally we multiply each of these vectors by the normalising matrix to generate the orthonormal basis coordinates as given below. Note that the basis and lattice vectors are given to full machine precision (14 significant figures). This will ensure that there are no errors in the results of the program due to rounding errors in the data. Also, if the data are given with lower precision, DMAREL may fail to find symmetry elements present. (For example, it may fail to find that the oxygen atoms lie on a 2 fold axis). The coordinates must be given to at least seven significant figures to avoid problems of this kind, although coordinates given to lower precision are acceptable if the ACCU directive is also used.
| BASI | ||||
| AL3+ | CORE | 0.0000000000000 | 0.0000000000000 | 0.3520000000000 |
| AL3+ | CORE | 0.0000000000000 | 0.0000000000000 | 0.1480000000000 |
| AL3+ | CORE | 0.0000000000000 | -0.0000000000000 | 0.6480000000000 |
| AL3+ | CORE | 0.0000000000000 | 0.0000000000000 | 0.8520000000000 |
| OX2- | CORE | -0.0709170692654 | 0.1057437733227 | 0.5833333333333 |
| OX2- | CORE | -0.0561182593567 | -0.1142878702072 | 0.5833333333333 |
| OX2- | CORE | 0.0709170692654 | -0.1057437733227 | 0.4166666666666 |
| OX2- | CORE | 0.1270353286222 | 0.0085440968844 | 0.5833333333333 |
| OX2- | CORE | 0.0561182593567 | 0.1142878702072 | 0.4166666666667 |
| OX2- | CORE | -0.1270353286222 | -0.0085440968845 | 0.4166666666667 |
BASIs and multipole input
See NEIGHBOURS
manual for details.