Background

The distributed multipole method has been used with great sucess on molecular dimers in isotlation [1]. DMAREL is a general purpose program aimed at extending this approach to the solid state. The code is based on an earlier program THBREL for ionic systems.

The program used the rigid molecule approximation and the P1 symmetry unit cell. The structure is minimised with respect to the position and orientation of the molecules and the size and shape of the unit cell.

Electrostatic sums for charges and dipoles are evaluated using the Ewald approach, higher multipolar interactions use a molecule based cut off for a direct summation. Other potential forms, referred to generally as short-range potentials are summed using an atom-based cut off.

The Minimisation Procedure

The minimisation routine is based on the Newton-Raphson technique. In a purely Newton-Raphson approach the minimiser would start with the initial positions first derivative vector (G) and second derivative matrix (the Hessian, W) to determine the step direction (d) via,

(1)

A full account of the derivatives and their implementation in DMAREL is given in reference [3].

On a purely quadratic surface this step would take us straight to the minimum energy position. However most surfaces are not purely quadratic and some iterative process must be used to find the nearest local minimum.

In DMAREL an iteration involves the choosing of a search direction and then estimation of the best distance to move in that direction by a series of line searches. For this reason the step direction defined by equation (1) is augmented by a scaling factor, a so that;

(2)

The job of the line search, then, is to choose the best value of a.. Line searches are discussed in the next section.

The equations describing the multipole interactions [2] and their implementation in DMAREL [3] are quite lengthy and so to date only the block diagonal terms of the second derivative matrix are coded. The inversion of the matrix required by equation (1) is also computationally intensive and hence time consuming. For these reasons after an initial calculation of the available terms (off diagonals being zeroed) the inverse of the second derivative matrix is updated from the history of the first derivatives using the Broydon, Fletcher, Powell algorithm [4].

Line Searches

Once the search direction is determined the step length to be taken in that direction must be considered carefully. The maximum allowed step is user controllable (MAXD and MAXT) and can greatly affect the rate and reliability of convergence. The initial step length used after a Hessian update will generally be that given by the Newton-Raphson equation (1) within the limits set. In order to approach the minimum efficiently we need to exploit the new search direction to the full and so a variety of line search methods are used to ensure that the best position along the search direction is found before another direction is chosen.

Linear Extrapolation, Interpolation And Negative Curvature

We can estimate the energy drop (GD) on taking a step in the search direction from the gradient vector and the step vector,

(3)

where we have written the gradient vector explicitly for clarity. The n in the GD label and as a subscript is used to indicate that the gradient is evaluated at the value of (1= initial position after update, 2= position after the latest move in the line search etc.). If we make the move suggested we arrive at a different point on the energy surface with a gradient G2 and can calculate a new estimated drop in energy GD2 for a further step in the search direction. Moves during line searches are made with copies of the atom coordinates so that all line search moves can be made relative to the starting point. Figure 1, Figure 2 and Figure 3 show the possible situations after the first step.

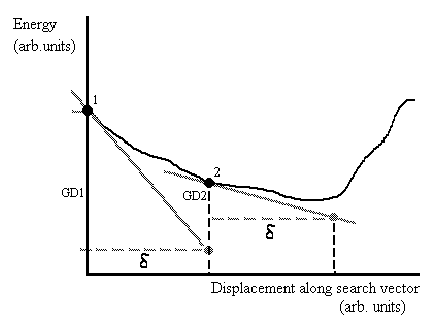
Figure 1

In Figure 1 GD1 and GD2 are both negative and |GD1| > |GD2|, in this case the step in the search direction has approached the minimum value possible along that line but not yet reached it. The program now immediately tests to see if a sufficient energy drop has occurred to justify a new search direction being chosen. The criterion used is,

(4)

If the this criterion is not met then a further step is made by extrapolation in the search direction.

Figure 2

In Figure 2 GD2 > 0 and so the step has passed over the minimum in the search direction. In this case a linear interpolation is made by scaling the initial step by the factor,

(5)

since GD1 is negative and GD2 positive, 0 < < 1, and the interpolation gives a point closer to the position (1 or 2) with the smaller magnitude gradient.

Figure 3

In Figure 3 GD2 < GD1 < 0 i.e. the gradient is becoming increasingly negative in the search direction and no minimum is near by. The program may continue the search to find more promising areas of the potential surface, but the run will be abandoned if the situation persists. There are several situations where persistent negative curvature may occur:

(1) The nearest energy minimum for the system is with all molecules removed to infinity, i.e. the gas phase. In this situation the program will fail with persistent negative curvature and the cell volume of the final position will be very large.

(2) An atom pair has been allowed to move into very close contact where the short range potential is unphysical. In the Buckingham potential at very short range the potential drops rapidly to minus infinity. This so called Buckingham catastrophe will result in negative curvature with a particulary close contact being reported by the CCLS output. The Buckingham parameters should be checked carefully, and the maximum step size made smaller.

If the criterion of equation (4) is not met further searches are conducted. The interpolated or extrapolated value of is used to calculate the gradient at the new positon and reset GD2, so that GD2 is always the last point to be tested. The old GD2 and are re-designated to GD3 and . Thus after one linear search has been performed three points on the energy surface have their gradients known with a values of 0, (the current search position), and 1. If the new value of GD2 also fails the test we can make a further interpolation or extrapolation, but now with the option of using a quadratic function defined by the last three points rather than the lines used in the linear searches. The search now assigns the minimum position of the quadratic to GD2 before performing the line search criterion test.