Three-Body
Interactions
These directives
are only use by a three-body run.
BOHA
| Operand types | I | F | F |
| Operand names | ILABEL | K3 | THETA0 |
ILABEL is an integer label giving the index of the three-body bond type. The same label is used in the THBO directive. ILABEL must be 1 for the first three-body bond type, 2 for the second, and so on up to a maximum of MAXTHB. The analytic form of the potential is
![]()
where ![]() is the bond angle in the crystal.
is the bond angle in the crystal. ![]() is in eV
is in eV ![]() ,
,
![]() is in
degrees.
is in
degrees. ![]() is a user defined equilibrium angle and is not necessarily the same as
the actual bond angle in the crystal. For example, in
is a user defined equilibrium angle and is not necessarily the same as
the actual bond angle in the crystal. For example, in ![]() quartz, the exact tetrahedral angle can be can be chosen for
quartz, the exact tetrahedral angle can be can be chosen for ![]() for the oxygen-silicon-oxygen bonds.
for the oxygen-silicon-oxygen bonds.
However, the actual
angles in the crystal deviate slightly from equilibrium. There is a restriction
that none of the bond angles in the crystal can be 180 degrees (see QART).
The cutoff chosen is cos(![]() )
> - 0.999. Also the equilibrium angle supplied
)
> - 0.999. Also the equilibrium angle supplied ![]() must be greater than acos(0.999) and less than acos(-0.999).
must be greater than acos(0.999) and less than acos(-0.999).
Printed output
THREE BODY FORCE CONSTANT WITH INDEX ILABEL
THE FORM OF THE THREE BODY POTENTIAL IS V = 1/2*K3* (THETA - THETA0)**2
K3 = K3 THETA0 = THETA0
Error messages
ERROR - A THREE BODY FORCE CONSTANT HAS BEEN DUPLICATEDThe integer ILABEL has already been used for another three-body bond.
ERROR - THE EQUILIBRIUM BOND ANGLE MUST BE GREATER THAN ARCCOS(0.999)
| Operand types | I | F | F |
| Operand names | ILABEL | K3 | THETA0 |
ILABEL is an integer label giving the index of the three-body bond type (see BOHA). The analytic form of the potential is
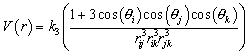
Printed output
THREE BODY FORCE CONSTANT WITH INDEX ILABEL
THE FORM OF THE THREE BODY POTENTIAL IS V = K3 * (1+3.0 * COS(THETAI) * COS(THETAJ) * COS(THETAK))/RIJ**3 * RIK**3 * RJK**3
K3 = K3 THETA0 = THETA0
Error messages
ERROR - A THREE BODY FORCE CONSTANT HAS BEEN DUPLICATED
The integer ILABEL has already been used for another three-body bond.
| Operand types | I | F | F | F | F |
| Operand names | ILABEL | K3 | RHO1 | RHO2 | THETA0 |
ILABEL is an integer label giving the index of the three-body bond type (see BOHA). The analytic form of the potential is
![]()
Where ![]() is
the bond angle in the crystal.
is
the bond angle in the crystal. ![]() is
in eV
is
in eV ![]() ,
,
![]() is
in degrees,
is
in degrees, ![]() and
and ![]() are in
are in ![]() .
.
![]() is a user defined equilibrium
angle and is not necessarily the same as the actual bond angle in the
crystal.
is a user defined equilibrium
angle and is not necessarily the same as the actual bond angle in the
crystal. ![]() and
and
![]() are
the bond lengths from the central atom i to the two peripheral
atoms j and k, that is the angle
are
the bond lengths from the central atom i to the two peripheral
atoms j and k, that is the angle ![]() .
.
Printed output
THREE BODY FORCE CONSTANT WITH INDEX ILABEL
THE FORM OF THE THREE BODY POTENTIAL IS V = 1/2*K3* (THETA - THETA0)**2 * EXP(-R/RHO1) * EXP(-R/RHO2)
K3 = K3 RHO1 = RHO1 RHO2 = RHO2
Error messages
ERROR - A THREE BODY FORCE CONSTANT HAS BEEN DUPLICATED
ERROR - THE EQUILIBRIUM BOND ANGLE MUST BE GREATER THAN ARCCOS(0.999)
| Operand types | I | F | F |
| Operand names | ILABEL | K3 | THETA0 |
ILABEL is an integer label giving the index of the three-body bond type (see BOHA). The analytic form of the potential is

Printed output
THREE BODY FORCE CONSTANT WITH INDEX ILABEL
THE FORM OF THE THREE BODY POTENTIAL IS V = 0.5* K3*(0.25*(THETA0-PI)**2-0.5*(THETA-PI)**2+0.25*((THETA-PI)**4) /((THETA0-PI)**2))
K3 = K3 THETA0 = THETA0
Error messages
ERROR - A THREE BODY FORCE CONSTANT HAS BEEN DUPLICATED
ERROR - THE EQUILIBRIUM BOND ANGLE MUST BE GREATER THAN ARCCOS(0.999) AND LESS THAN ARCCOS(-0.999)
| Operand types | I | F | F |
| Operand names | ILABEL | K3 | THETA0 |
ILABEL is an integer label giving the index of the three-body bond type (see BOHA). The analytic form of the potential is very complex, it is given below for the sake of completeness.
![]()
Where
Where
![]() is
the bond angle in the crystal,
is
the bond angle in the crystal, ![]() is in eV
is in eV ![]() ,
,
![]() is
in degrees.
is
in degrees. ![]() is a user defined equilibrium angle and is not necessarily the same
as the actual bond angle in the crystal. This potential may be used
when
is a user defined equilibrium angle and is not necessarily the same
as the actual bond angle in the crystal. This potential may be used
when ![]() is
180 degrees, but not when
is
180 degrees, but not when ![]() is 180 degrees (see BOHZ). It is designed
so that the second derivative of V with respect to
is 180 degrees (see BOHZ). It is designed
so that the second derivative of V with respect to ![]() is
the same as for BOHA
when
is
the same as for BOHA
when ![]() .
Also the first derivative of V with respect to
.
Also the first derivative of V with respect to ![]() tends to zero as
tends to zero as ![]() tends
to
tends
to ![]() .
This allows the derivative to be calculated using a power series approximation.
.
This allows the derivative to be calculated using a power series approximation.
Printed output
THREE BODY FORCE CONSTANT WITH INDEX ILABEL
THE FORM OF THE THREE BODY POTENTIAL IS V = SIXTH ORDER POLYNOMIAL IN THETA WITH CORRECT LIMITS AT THETA = PI AND THETA = 0
K3 = K3 THETA0 = THETA0
Error message
ERROR - A THREE BODY FORCE CONSTANT HAS BEEN DUPLICATED
| Operand types | I | F | F |
| Operand names | ILABEL | K3 | THETA0 |
ILABEL is an integer label giving the index of the three-body bond type (see BOHA). The analytic form of the potential is
Where ![]() is the bond angle in the crystal,
is the bond angle in the crystal, ![]() is in eV
is in eV ![]() .
The equilibrium angle is
.
The equilibrium angle is ![]() .
This allows linear bonds to be treated. The derivatives are again calculated
using a power series if
.
This allows linear bonds to be treated. The derivatives are again calculated
using a power series if ![]() is close to
is close to ![]() .
.
Printed output
THREE BODY FORCE CONSTANT WITH INDEX ILABEL
THE FORM OF THE THREE BODY POTENTIAL IS V = 1/2*K3* (THETA - PI)**2
K3 = K3 THETA0 = THETA0
Error messages
ERROR - A THREE BODY FORCE CONSTANT HAS BEEN DUPLICATED
THRH
| Operand types | I | F | F | F | F |
| Operand names | ILABEL | K3 | THETA0 | R01 | R02 |
ILABEL is an integer label giving the index of the three-body bond type (see BOHA). The analytic form of the potential is
![]()
Where
![]() is in
eV
is in
eV ![]() .
.
![]() is the
bond angle in the crystal.
is the
bond angle in the crystal. ![]() is
in degrees.
is
in degrees. ![]() is
a user defined equilibrium angle and is not necessarily the same as the
actual bond angle in the crystal. r01 and r02 are in
is
a user defined equilibrium angle and is not necessarily the same as the
actual bond angle in the crystal. r01 and r02 are in ![]() and are the equilibrium bond lengths of the ij and ik bonds
respectively.
and are the equilibrium bond lengths of the ij and ik bonds
respectively.
| Operand types | I | F | F | F |
| Operand names | ILABEL | K3 | R01 | R02 |
ILABEL is an integer label giving the index of the three-body bond type (see BOHA). The analytic form of the potential is
![]()