XClose

Rough Path and Machine Learning Research Group

Menu

Synthetic Time Series Generation

Background and Motivation

Synthetic data generation has achieved increasing attention as it provides an effective way to preserve data privacy while keeping key statistical properties of data.  Time series are ubiquitous nowadays and it has many examples in our daily life, ranging from finance to medicine. Synthetic time series generations are powerful and emerging technologies to accelerate the deployment of the ML in finance. 

Project objectives

The goal of this project is to build, through collaboration with academic and industrial partners, mathematical and computational toolsets based around the expected signature of a stochastic process for generating synthetic time series data, and to validate its usefulness and effectiveness on the empirical financial data.

Methodologies and Research findings

Wasserstein GANs

Generative adversarial networks (GANs) provide a deep learning framework for synthetic data generation. It is composed of a generator and discriminator, parameterized by deep neural networks; the generator tries to learn a model from the noise vector to target data while the discriminator aims to discriminate the synthetic data and real data. By alternatively optimizing the generator and discriminator until the discriminator struggles to differentiate real/generated data, GAN models are trained to generate realistic fake data to mimic the distribution of real data.  The flowchart of GANs can be found in the below figure.   

wgan

 

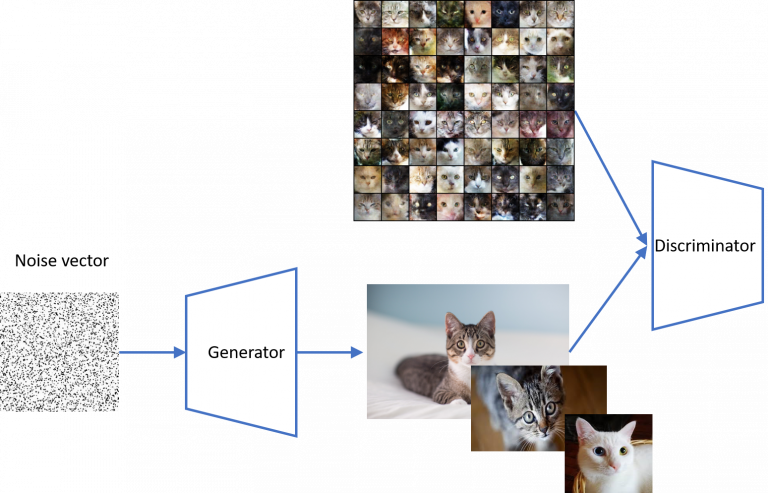
Inspired by Wasserstein distance of two distributions, Wasserstein GANs (WGANs) utilize Wasserstein distance as the discriminator, where the test function is approximated by deep neural network. WGAN have achieved superior performance in generating high-quality synthetic image data. However, time series generation using WGAN is still very challenging due to high dimensionality of time series and complex spatial-temporal dependency. Moreover, the min-max formulation of GANs is computationally expensive and the training process might not be very stable.

Sig-Wasserstein GANs 

To address the above challenges of WGANs, in [1] we develop novel and high-quality time-series generators, the so-called Sig-Wasserstein GANs (SigWGANs), by combining continuous-time stochastic models with the newly proposed signature W1 metric. The former is the Logsig-RNN model based on the stochastic differential equations, whereas the latter originates from the universal and principled mathematical features to characterize the measure induced by time series. In particular, the signature of a path is a graded sequence of statistics to provide a top-down description of time series, and its expected value characterises the law of the time series.  SigWGAN allows simplifying WGAN's min-max game into an optimization problem and reducing computational cost signficanatly while generating high fidelity samples. The proposed SigWGAN can handle irregularly spaced data streams of variable lengths and is poetically efficient for data sampled at high frequency. Compared with other state-of-the-art methods, SigWGAN has better robustness to generate the synthetic data in different sampling frequencies. 

Conditional Sig-Wasserstein GANs

As described before, GANs may struggle to learn the temporal dependence of joint probability distributions induced by time-series data. In particular, long time-series data streams hugely increase the dimension of the target space, which may render generative modelling infeasible. To overcome this challenge, motivated by the autoregressive models in econometric, we propose the generic conditional Sig-WGAN, which takes the past path as conditioning variables and simulate future time series to mimic the conditional distribution under the true measure. Our model extends the SigWGAN framework to the conditional setting and adds a supervised learning module to learn the expected signature of the future path under the true measure prior to generative training. More specifically, we develop a new metric, conditional Sig-W1, that captures the conditional joint law of time series models, and use it as a discriminator. The signature feature space enables the explicit representation of the proposed discriminators which alleviates the need for expensive training. Numerical results on both synthetic and empirical S&P500 and DJI datasets demonstrate that our method consistently and significantly outperforms state-of-the-art benchmarks with respect to test metrics of similarity and predictive performance.

Reference

  1.  Ni, H., Szpruch, L., Sabate-Vidales, Xiao, B., M., Wiese, M., and Liao, S.; Signature-Wasserstein GANs for time series generation. Accepted by 2nd ACM International Conference on AI in Finance, 2021.  
  2. Ni, H., Szpruch, L., Wiese, M., Liao, S. and Xiao, B.; Conditional Sig-Wasserstein GANs for time series generation. arXiv preprint arXiv:2006.05421. 2020.